Ergodicity problem in economics

Hey folks!

Music I’m listening to - Down Where I'm going

Let’s dive into a little bit of what theories shaped economics the way it is today.

A Simple Gamble

Toss a coin, and for heads you win 50% of your wealth , for tails you lose 40%.

Formally, any decision we make is taken as a gamble, be it a school for your child or deciding on matters of taxation.

We’ll take a look at how treatment for the gambling problems have evolved from 1700’s.

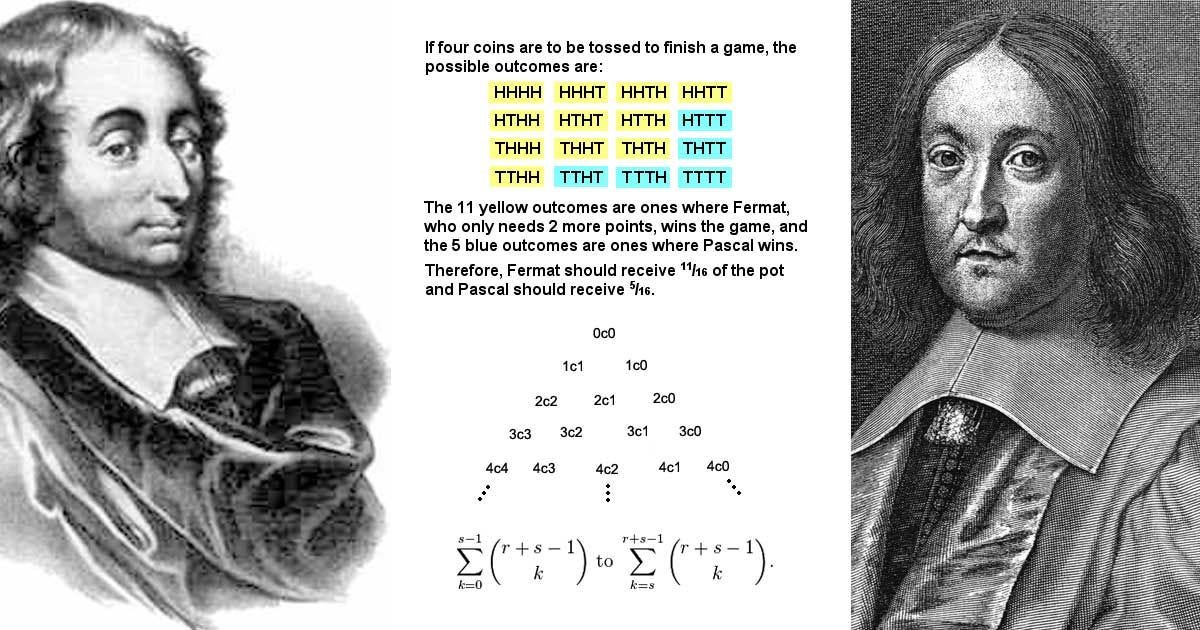
Expectation Value

The exchange of letters between Pascal and Fermat in 1654 has started the actual development in probability theory. They were trying to solve a moral problem of assessing people’s hopes and expectations in a fair way.

Few years later, a rule of thumb had been developed. It predicts that given the choice between two gambles, we pick the greater expected wealth change (∆x). People would generally accept the above gamble according to this theory.

Expected Utility Theory

In real life, would people risk giving away 40% of their house,car and life savings at the toss of a coin?

To answer the above paradox, Bernoulli updated the above theory: they don’t consider the expected changes in wealth (x), but the expected changes in usefulness of wealth, u(x). Basically utility function encodes the psychology of an individual.

The above theory considers static probability space, without an explicit treatment of time. Bernoulli and his followers, didn’t discuss the rate of change of utilities but only magnitude of changes.

A Modern Treatment Asking The Ergodicity Question

First step, we consider financial decisions without uncertainty. In the second step, we generalize by introducing noise.

Additive growth rate - If a company is paying 12000 per year versus 2000 per month. I would choose the 2000 one because I can maximize ∆x/∆t

Exponential growth rate - If the savings account pays 4% per year and 1% per month, it’s again the growth rate I would maximize ∆lnx/∆t

The dynamics in which the person is a part of has more to do, than the psychology of an individual.

The relevant growth rates are ergodic observables of their respective processes. By design, their (time or ensemble) average tells us what tends to happen over time.

This exposes expected wealth model as physically naive. It doesn’t reflect what happens over time. Expected utility theory overlooked the physical problem and jumped to psychological arguments, which tend to be circular and hard to constrain.

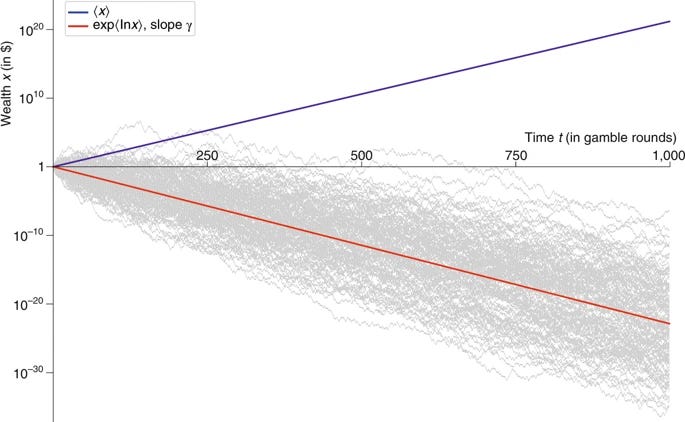
The blue line tells the ensemble narrative of expected wealth model (which is heavily skewed towards few fat tail winners and most of them losing their wealth )and the red line (ergodic growth rate) tells us what happens to a typical individual trajectory.

Growth rate optimization is sometimes called ergodic economics. It does not mean ergodicity is assumed - quite the opposite. It refers to doing economics by asking explicitly whether something is ergodic, which isn’t often the case.

The above research was published in nature few years back by Ole B Peters (research paper) and has implications in how we view the markets, interactions and populations.

We’ll probably explore more on that next time.